Navigáció: Főoldal / III. rész / III. rész (2. fejezet)

III. rész: Részletes összehasonlítás (folytatás)

2. A tartalmi jelölés

2.1. A tartalmi jelölés elemeiről általában

Ebben a fejezetben részletesen megismerkedünk a MathML tartalmi elemeivel.

Tartsuk szem előtt a következőket:

A MathML tartalmi elemek “nem hajtják végre” magát a matematikai számítást vagy műveletet, a böngészőben nem fogjuk egy számítás eredményét látni, hiszen a tartalmi elemek csak dokumentálási célokra használhatók.
A tartalmi elemek ugyan helyesen jelenítik meg a matematikai kifejezéseket, de elsősorban azok tartalmát hivatottak bemutatni. Ha nincs szükségünk a valós tartalomra, akkor inkább használjuk a már megismert megjelenítő elemeket.

Ha egy MathML kifejezést fel kívánunk használni valamilyen más alkalmazásban, akkor célszerű a tartalmi jelölést használni, hiszen ekkor a kiválasztott alkalmazás képes lehet magát a műveletet elvégezni is, így kímélve meg minket sok felesleges munkától.

A tartalmi elemek mindegyike megkaphatja a class, style, id és other attribútumokat. Az első három megegyezik a HTML hasonló attribútumaival és a stíluslapokkal (CSS) kapcsolatos. Az other olyan dolgok leírására alkalmas, melyre nincs külön specifikáció a MathML-ben (például a megjelenítés formájára vonatkozó megjegyzések, stb.). Használatakor vegyük figyelembe, hogy a legtöbb megjelenítő figyelmen kívül hagyja a tartalmát.

A legtöbb (de nem mind!) tartalmi elem megkaphatja a definitionURL attribútumot is, melyben egy olyan URL adható meg, ahol az adott elem (bővebb) szemantikai leírása található meg. Formájára nincs szabály, alapértelmezése sincs.

Ezeknek az attribútumoknak sem az OpenMath-ban, sem a T_EX-ben nincs megfelelőjük, mert egyiknél sem használunk a MathML-nek megfelelő stíluslapokat. A T_EX-nek van saját stíluslapja, melyet a \documentstyle parancs segítségével használhatunk (Lásd a III/1.2.1. A token-elemek attribútumai című fejezetet). Az OpenMath-nál nincsenek külön stíluslapok, a Content Dictionarykben (CD) adunk meg minden paramétert. Ezekben a CD-kben osztályozhatjuk az elemek paramétereit. Az egyes CD-k tartalmát a C Függelék tartalmazza.

2.2. Tokenelemek

2.2.1. Számok

A <cn> elemet használjuk numerikus állandók specifikálására. Alapértelmezésként bármilyen tízes számrendszerbeli valós érték lehet, leírásakor tízes számrendszerbeli számokat, tizedespontot, előjelet, esetleg előre definiált szimbolikus konstansokat (π) alkalmazhatunk.

Attribútumai a következők lehetnek: type, base. A type segítségével határozhatjuk meg a leírni kívánt szám típusát, értéke “real”, “integer”, “rational”, “complex-cartesian”, “complex-polar”, “constant” lehet. Alapértelmezése a “real”. A base a szám alapszámrendszerét adja meg, 2 és 36 közötti értéket vehet fel, alapértelmezése “10”.

Racionális és komplex számok esetén az egyes számrészek elválasztására a <sep/> elem használandó.

Alapállapotban az így meghatározott számok úgy jelennek meg, mintha azokat az <mn> elemmel írtuk volna le.

T_EX-ben ugyanazok érvényesek, amelyeket a megjelenítő elemeknél megismertünk.

OpenMath esetén több lehetőségünk van. Egész számok megadására használjuk az <OMI> elemet, melynél fontos, hogy a pozitív előjelet nem használjuk, valamint az adott számot megadhatjuk 16-os számrendszerben is, de ekkor “x”-szel kell kezdenünk (pl: "x2D4"). Nem egész számok esetén használjuk az <OMF/> elemet. Az elem dec vagy hex paraméterében adhatjuk meg a számot, a számrendszerétől függően. Természetesen előfordulhat, hogy egy, a MathML-ben számként leírt “objektum” az OpenMath-ban máshogy írandó le (legtöbbször valamilyen szimbólumként, az <OMS/> elemmel). Ezen kívül lehetőségünk van egy <OMATTR> elemben megadni a számra vonatkozó típust, ilyenkor a cd=”nums” attribútumot kell beállítani, és megadni a megfelelő számtípust, ami “based_integer”, “complex_cartesian”, “complex_polar”, “e”, “gamma”, “i”, “infinity”, “NaN”, “pi” és “rational” lehet.

Lássunk néhány példát az egyes típusokra (első a MathML, második a T_EX, harmadik az OpenMath forma):

$12345.7$

<cn type="real"> 12345.7 </cn>
 
12345.7
 
<OMF dec=”12345.7”/>

$12345$

<cn type="integer"> 12345 </cn>
 
12345
 
<OMI>12345</OMI>

$AB3 alsóindex 16$

<cn type="integer" base=16> AB3 </cn>
 
AB3_16
 
<OMI>xAB3</OMI>

$12432/2342342$

<cn type="rational> 12342 <sep/> 2342342 </cn>
 
12342/2342342
 
<OMF dec=”5,269e-3”/>

$12.3+5i$

<cn type="complex-cartesian"> 12.3 <sep/> 5 </cn>
 
12.3+5i
 
<OMATTR>
  <OMATP>
    <OMS cd=”nums” name=”complex_cartesian”/>
  </OMATP>
  <OMF dec=”12.3+5i”/>
</OMATTR>

$Polar(2,3.1415)$

<cn type="complex-polar"> 2 <sep/> 3.1415 </cn>
 
\text{Polar} (2,3.1415)
 
<OMATTR>
  <OMATP>
    <OMS cd=”nums” name=”complex_polar”/>
  </OMATP>
  <OMA>
    <OMI>2</OMI>
    <OMF dec=”3.1415”/>
  </OMA>
</OMATTR>

$pi$

<cn type="constant"> &pi; </cn>
 
\pi
 
<OMS cd=”nums” name=”pi”/>

2.2.2. Azonosítók

A <ci> elem szimbolikus nevek leírására használatosak. Ezek általában valamilyen matematikai objektumok azonosítói. Alapállapotban az így meghatározott azonosítók úgy jelennek meg, mintha azokat az <mi> elemmel írtuk volna le.

Egyetlen saját attribútuma van, a type, melynek segítségével határozhatjuk meg a leírni kívánt azonosító típusát, értéke “real”, “integer”, “rational”, “complex-cartesian”, “complex-polar”, “constant”, valamint “interval”, “list”, “matrix”, “matrixrow”, “set”, “vector”, “apply”, “reln”, “lambda”, “fn” lehet. Alapértelmezése a “”, azaz nincs meghatározva.

T_EX-ben ugyanazok érvényesek, amelyeket a megjelenítő elemeknél megismertünk.

OpenMath-ban az <OMV/> elemet használjuk az azonosítók leírására. Egyéb attribútumok (pl. indexek) megadására az <OMATTR> és <OMATP> elem pár használatos, melyeket a változó előtt adunk meg. Az <OMATTR> elem jelzi az attribútum megadását, az <OMATP> elem pedig leírja magát, az attribútumot. Hosszabb azonosítóknál használhatjuk az <OMSTR>, valamint az <OMB> elemeket is. Az előbbi egy szöveget, az utóbbi egy bájtsorozatot (betűk, számok, valamint a “+”, “-” “/” “=” jelek) tartalmazhat.

Íme néhány példa:

$x$

<ci> x </ci>
 
x
 
<OMV name=”x”/>

$V (vektor)$

<ci type="vector"> V </ci>
 
\bold V
 
<OMATTR>
  <OMATP>
    <OMS cd=”ecc” name=”type”/>
    <OMS cd=”ecc” name=”array”/>
  </OMATP>
  <OMV name=”V”/>
</OMATTR>

$x alsóindex a$

<ci>
  <msub>
    <mi>x</mi>
    <mi>a</mi>
  </msub>
</ci>
 
x_a
 
<OMA>
  <OMATTR>
    <OMATP>
      <OMS cd=”presentation” name=”style”/>
      <OMSTR> subscripted <OMSTR>
    </OMATP>
    <OMV name=”x”/>
  </OMATTR>
  <OMV name="a"/>
</OMA>

2.3. Tartalmi elemek csoportba rendezése

Az <apply> elem egy függvény vagy művelet argumentumaival való megjelenítésére szolgál. A MathML tartalmi elemek legnagyobb részét egy ilyen elemmel vezetjük be (funkciójában hasonlít a megjelenítő <mrow> elemre). Az <apply> elem első attribútuma mindig az a művelet, amelyet meg szeretnénk valósítani, ezután következnek a művelet argumentumai. Használata nagymértékben függ attól az elemtől, melyre vonatkozik. Nincs definitionURL attribútuma!

T_EX-ben ennek az elemnek leginkább a {} felel meg, de az esetek nagy részében nincs szükség a használatára.

OpenMath-ban az <OMA> elem a megfelelője. Itt is az első argumentum mindig az a művelet (szimbólum), amelyet meg szeretnénk valósítani, ezután következnek a művelet argumentumai.

Példák:

$3!$

<apply>
  <factorial/>
  <cn>3</cn>
</apply>
 
3!
 
<OMA>
  <OMS cd=”arith” name=”factorial”/>
  <OMI>3</OMI>
</OMA>

$3+4$

<apply>
  <plus/>
  <cn>3</cn>
  <cn>4</cn>
</apply>
 
3+4
 
<OMA>
  <OMS cd=”arith” name=”plus”/>
  <OMI>3</OMI>
  <OMI>4</OMI>
</OMA>

$sin x$

<apply>
  <sin/>
  <ci>x</ci>
</apply>
 
\sin x
 
<OMA>
  <OMS cd=”trans” name=”sin”/>
  <OMV name=”x”/>
</OMA>

2.4. Deklarációk

A <declare> elemnek két fontos szerepe van: az egyik, hogy megváltoztassuk vagy megadjuk az alapértelmezését egy adott kifejezésnek, a másik, hogy kapcsolatot létesítsünk egy név és egy objektum között. Tipikus használata számítógépes algebra esetén lehetséges.

A <declare>-nek egy vagy két argumentuma lehet, az első egy <ci>-ben leírt azonosító, a második (opcionálisan) egy objektum, mellyel inicializáljuk a változót:

<declare type="vector">
  <ci> V </ci>
  <vector>
    <cn> 1 </cn>
    <cn> 2 </cn>
    <cn> 3 </cn>
  </vector>
</declare>

Az objektum típusának és a deklarált elem típusának meg kell egyeznie. Például, ha az attribútumban “fn”-nek deklaráltuk a változót, akkor az objektumnak is valamilyen függvény-típusúnak kell lennie. Ha deklarációkor nem határozunk meg típust, akkor az objektum típusát vesszük alapértelmezésnek.

Alapértelmezésben érvényessége “local”, azaz helyi, az adott MathML elemre vonatkozó. Ezt a scope attribútum “global”-ra állításával kiterjeszthetjük az egész dokumentumra (a nyitó <math> elemtől kezdődően).

További attribútumok: type, mely a deklaráció típusát határozza meg, bármilyen tartalmi azonosító lehet, alapértelmezése “ci”. A nargs attribútum a függvénydeklaráció argumentumainak számát határozza meg, alapértelmezése 1. Az occurence attribútumban adjuk meg a műveletekbeli szerepet, értéke “prefix”, “infix” vagy “function-model” lehet, ez utóbbi az alapértelmezése.

A <bvar> elemet használjuk az egyes műveletek alapváltozóinak leírásához. Tartalmazhat egy <degree> elemet is, mellyel a változó foka adható meg.

T_EX-ben nincs szükség ilyen parancsra, helyette egyszerűen leírjuk az adott kifejezést.

OpenMath-ban ezeket az elemeket <OMS/> és <OMV/> elemek kombinációjával helyettesíthetjük.

$f(x,y)=(F+G)(x,y)$

<declare type="fn" nargs="2" scope="local">
  <ci> f </ci>
  <apply>
    <plus/>
    <ci> F </ci>
    <ci> G </ci>
  </apply>
</declare>
 
f\left(x,y\right)=\left(F+G\right)\left(x,y\right)
 
<OMA>
  <OMS cd = "relation" name="eq"/>
  <OMA>
    <OMV name="f"/>
    <OMATTR>
      <OMATP>
        <OMS cd="presentation" name="left"/>
        <OMSTR>(</OMSTR>
        <OMS cd="presentation" name="right"/>
        <OMSTR>)</OMSTR>
      </OMATP>
      <OMA>
        <OMS cd = "linalg" name="vector"/>
        <OMV name="x"/>
        <OMV name="y"/>
      </OMA>
    </OMATTR>
  </OMA>
  <OMA>
    <OMS cd = "arith" name="times"/>
    <OMATTR>
      <OMATP>
        <OMS cd="presentation" name="left"/>
        <OMSTR>(</OMSTR>

                       <OMS cd="presentation" name="right"/>
        <OMSTR>)</OMSTR>
      </OMATP>
      <OMA>
        <OMS cd = "arith" name="plus"/>
        <OMV name="F"/>
        <OMV name="G"/>
      </OMA>
    </OMATTR>
    <OMATTR>
      <OMATP>
        <OMS cd="presentation" name="left"/>
        <OMSTR>(</OMSTR>
        <OMS cd="presentation" name="right"/>
        <OMSTR>)</OMSTR>
      </OMATP>
      <OMA>
        <OMS cd = "linalg" name="vector"/>
        <OMV name="x"/>
        <OMV name="y"/>
      </OMA>
    </OMATTR>
  </OMA>
</OMA>

$J(x)=ln x$

<declare type="fn">
  <ci> J </ci>
  <lambda>
    <bvar>
      <ci> x </ci>
    </bvar>
    <apply>
      <ln/>
      <ci> x </ci>
    </apply>
  </lambda>
</declare>
 
J\left(x\right)=\ln x
 
<OMA>
  <OMS cd = "relation" name="eq"/>
  <OMA>
    <OMS cd = "arith" name="times"/>
    <OMV name="J"/>
    <OMATTR>
      <OMATP>
        <OMS cd="presentation" name="left"/>
        <OMSTR>(</OMSTR>
        <OMS cd="presentation" name="right"/>
        <OMSTR>)</OMSTR>
      </OMATP>
      <OMV name="x"/>
    </OMATTR>
  </OMA>
  <OMA>
    <OMS cd="transc" name="ln"/>
    <OMV name="x"/>
  </OMA>
</OMA>

$integrál 0 a f(x) dx$

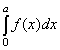
<apply>
  <int/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <lowlimit>
    <cn> 0 </cn>
  </lowlimit>
  <uplimit>
    <ci> a </ci>
  </uplimit>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\int\limits_0^a f(x)dx
 
<OMA>
  <OMS cd="calculus" name="defint"/>
  <OMA>
    <OMS cd="interval" name="interval"/>
    <OMI>0</OMI>
    <OMV name="a"/>
  </OMA>
  <OMA>
    <OMS cd = "arith" name="times"/>
    <OMA>
      <OMS cd = "arith" name="times"/>
      <OMA>
        <OMV name="f"/>
        <OMATTR>
          <OMATP>
            <OMS cd="presentation" name="left"/>
            <OMSTR>(</OMSTR>
            <OMS cd="presentation" name="right"/>

                           <OMSTR>)</OMSTR>
          </OMATP>
          <OMV name="x"/>
        </OMATTR>
      </OMA>
      <OMV name="d"/>
    </OMA>
    <OMV name="x"/>
  </OMA>
</OMA>

2.5. Aritmetika, algebra, logika

2.5.1. Alapműveletek

Az összeadás, kivonás, szorzás, osztás leírására MathML-ben rendre a <plus/>, a <minus/>, a <divide/> és a <power/> elemeket használjuk.

A <plus/> elemnek több argumentuma lehet, a többinek kizárólag kettő. Bár a <minus/> esetén egy argumentummal lehetőségünk van leírni a negatív számokat, de ezt kerüljük el, helyette a <cn> elemmel jelöljük a negatív számokat.

T_EX-ben az összeadás, a kivonás jelölésére a “+” és “-” jelet használjuk. Szorzás jelölésére – ha szükség van rá – a \cdot parancsot használjuk, ekkor látható lesz a szorzásjel. Az osztás leírására a törtek-nél ismertetett parancsokat használjuk.

OpenMath-ban az alapműveleteket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “minus”, “plus”, “times”, “divide” paraméterekre állításával) helyettesítjük. A szükséges CD minden esetben az “arith”.

$x+y+z$

<apply>
  <plus/>
  <ci> x </ci>
  <ci> y </ci>
  <ci> z </ci>
</apply>
 
x+y+z
 
<OMA>
  <OMS cd=”arith” name=”plus”/>
  <OMV name=”x”/>
  <OMV name=”y”/>
  <OMV name=”z”/>
</OMA>

$x-y$

<apply>
  <minus/>
  <ci> x </ci>
  <ci> y </ci>
</apply>
 
x-y
 
<OMA>
  <OMS cd=”arith” name=”minus”/>
  <OMV name=”x”/>
  <OMV name=”y”/>
</OMA>

$ab$

<apply>
  <times/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
ab
a\cdot b
 
<OMA>
  <OMS cd=”arith” name=”times”/>
  <OMV name=”a”/>
  <OMV name=”b”/>
</OMA>

$a/b$

<apply>
  <divide/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
\frac a b
 
<OMA>
  <OMS cd=”arith” name=”divide”/>
  <OMV name=”a”/>
  <OMV name=”b”/>
</OMA>

2.5.2. Fontosabb aritmetikai, algebrai műveletek

A hatványozás leírására a <power/> elemet használjuk. Argumentumaiban először az alapot, aztán a kitevőt kell megadni. A <root/> elemet használjuk a gyökvonás leírásához. Egy vagy két argumentuma lehet, ha kettő van, akkor az első mindig egy <degree> elem, mely a gyökkitevőt adja meg. Ha nem adjuk meg a <degree> elemet, akkor a gyökkitevő alapértelmezése 2 lesz.

Az osztás maradékának leírásához a <rem/> elemet használjuk, az egész rész meghatározására pedig a <quotient/> elem szolgál. Mindkettőnek két argumentuma van.

Az abszolút érték leírására az <abs/> elemet használjuk.

A <gcd/> elem a legnagyobb közös osztó leírására szolgál, több argumentuma lehet. Faktoriálisok leírására a <factorial/> elemet használjuk, egyetlen argumentuma lehet.

Az <interval> elem egy valós intervallumot ír le. Egyetlen saját attribútuma van, a closure, mely az intervallum zártságát írja le és a következő értékeket veheti fel: “open”, “closed”, “open-closed”, “closed-open”. Alapértelmezés a “closed”. Nincs definitionURL attribútuma!

A <conjugate/> egy argumentumú elemet használjuk a konjugált komplex gyök leírásához.

T_EX-ben a hatványozást egyszerűen a “^” jellel írjuk le. A gyökvonásra viszont két parancsunk van. Ha négyzetgyököt kell írnunk használjuk az \sqrt parancsot, mely után kapcsos zárójelekben kell megadni a kifejezést. Ha nem négyzetgyökre van szükségünk, akkor használjuk a \root - \of parancspárt, ahol \root után kell megadni a kitevőt, az \of után pedig a kifejezést.

A maradék jelölésére a \bmod parancsot, az egész rész leírására pedig a “[”, “]” zárójelpárt használjuk, Az abszolút értéket pedig egyszerűen a “|” jellel jelöljük.

A konjugált komplex gyök leírásához használjuk az \overline parancsot, mely után kapcsos zárójelek között kell megadni a kifejezést.

A többi elemnek nincsen megfelelője, ezeket a kinézetüknek megfelelően kell leírni.

OpenMath-ban a <power/>, a <root/>, a <rem/>, a <quotient/>, <abs/>, a <factorial/> és a <conjugate/>, <gcd/> elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “power”, “root”, “rem”, “quotient”, “abs”, “factorial”, “conjugate”, “gcd” beállításával) helyettesítjük. A “root” attribútum esetén az <OMS/> elem első argumentuma a kitevő. A szükséges CD “factorial”, “gcd”, “quotient”, “rem” esetén “integer”, egyébként “arith”.

Az <interval/> elemnek az “interval” CD-ben szereplő “inteval_cc”, “interval_co”, “interval_oc”, “interval_oo” attribútumok felenek meg (“c” – zárt, “o” – nyílt).

Példák:

$x a harmadikon$

<apply>
  <power/>
  <ci> x </ci>
  <cn> 3 </cn>
</apply>
 
x^3
 
<OMA>
  <OMS cd=”arith” name=”power”/>
  <OMV name=”x”/>
  <OMI> 3 </OMI>
</OMA>

$a az n-edik gyök alatt$

<apply>
  <root/>
  <degree>
    <ci> n </ci>
  </degree>
  <ci> a </ci>
</apply>
 
\root n\of a
 
<OMA>
  <OMS cd=”arith” name=”root”/>
  <OMV name=”n”/>
  <OMV name=”a”/>
</OMA>

$a mod b$

<apply>
  <rem/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
a\mod b
 
<OMA>
  <OMS cd=”integer” name=”rem”/>
  <OMV name=”a”/>
  <OMV name=”b”/>
</OMA>

$[a/b]$

<apply>
  <quotient/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
\left[ a/b \right]
 
<OMA>
  <OMS cd=”integer” name=”quotient”/>
  <OMV name=”a”/>
  <OMV name=”b”/>
</OMA>

$|x|$

<apply>
  <abs/>
  <ci> x </ci>
</apply>
 
|x|
 
<OMA>
  <OMS cd=”arith” name=”abs”/>
  <OMV name=”x”/>
</OMA>

$(a;b;c)$

<apply>
  <gcd/>
  <ci> a </ci>
  <ci> b </ci>
  <ci> c </ci>
</apply>
 
\gcd\left(a;b;c\right)
 
<OMA>
  <OMS cd="integer" name="gcd">
  <OMATTR>
    <OMATP>
      <OMS cd="presentation" name="left"/>
      <OMSTR>(</OMSTR>
      <OMS cd="presentation" name="right"/>
      <OMSTR>)</OMSTR>
    </OMATP>
    <OMA>
      <OMS cd = "linalg" name="vector"/>
      <OMV name="a"/>
      <OMV name="b"/>
      <OMV name="c"/>
    </OMA>
  </OMATTR>
</OMA>

$n!$

<apply>
  <factorial/>
  <ci> n </ci>
</apply>
 
n!
 
<OMA>
  <OMS cd=”integer” name=”factorial”/>
  <OMV name=”n”/>
</OMA>

$(a,b]$

<interval closure="open-closed">
  <ci> a </ci>
  <ci> b </ci>
</interval>
 
\left(a,b\right]
 
<OMA>
  <OMS cd="interval" name="interval_oc"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$x+iy felülvonással$

<apply>
  <conjugate/>
  <apply>
    <plus/>
    <ci> x </ci>
    <apply>
      <times/>
      <cn> &ImaginaryI; </cn>
      <ci> y </ci>
    </apply>
  </apply>
</apply>
 
\overline{x+iy}
 
<OMA>
  <OMS cd=”arith” name=”conjugate”/>
  <OMA>
    <OMS cd=”arith” name=”plus”/>
    <OMV name=”x”/>
    <OMA>
      <OMS cd=”arith” name=”times”/>
      <OMV name=”i”/>
      <OMV name=”y”/>
    </OMA>
  </OMA>
</OMA>

2.5.3. Fontosabb aritmetikai, algebrai függvények

A <max/> és a <min/> elemeket használjuk a maximum és minimum függvények leírásához, több argumentuma lehet.

A logaritmusfüggvények leírására alaptól függően az <ln/> és a <log/> elemeket használhatjuk. Az <ln/> elemet használjuk a természetes alapú, a <log/> elemet pedig az n alapú logaritmus-függvény leírásához. Az előbbinek egy, az utóbbinak egy vagy két argumentuma lehet, ha kettő, akkor az elsőnek egy <logbase> elemnek kell lennie, mely megadja a logaritmus alapját. Ha ez nincs megadva, akkor alapértelmezése a 10 lesz.

Az <exp/> elem az exponenciális függvénynek (az ln függvény inverze) felel meg ( $exp(1)=2.718281828$ ), egyetlen argumentuma van.

T_EX-ben a minimum- és maximum-függvényekre a \max és a \min parancsokat használjuk.

A logaritmus-függvényekre három parancs áll rendelkezésünkre, az \ln (a természetes alapúra), az \lg (a tízes alapúra) és a \log (az n alapúra), mely utóbbi után alsó indexben (\log_n) megadhatjuk az alapot. Az exponenciális-függvénynek pedig az \exp parancs felel meg.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “max”, “min”, “ln”, “log”, “exp” beállításával) helyettesítjük. A szükséges CD a “max” és “min” esetében a “minmax”, a többinél a “transc”.

$max{a,b}$

<apply>
  <max/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
\max\left\{a,b\right\}
 
<OMA>
  <OMS cd=”minmax” name=”max”/>
  <OMV name=”a”/>
  <OMV name=”b”/>
</OMA>

$min alsóindex x {x a négyzeten, ahol x nem eleme a B halmaznak}$

<apply>
  <min/>
  <bvar>
    <ci>x</ci>
  </bvar>
  <condition>
    <reln>
      <notin/>
      <ci> x </ci>
      <ci type="set"> B </ci>
    </reln>
  </condition>
  <apply>
    <power/>
    <ci> x </ci>
    <cn> 2 </cn>
  </apply>
</apply>
 
\min_x\left\{x^2\mid x\notin B
 
<OMA>
  <OMATTR>
    <OMATP>
      <OMS cd=”presentation” name=”style”/>
      <OMSTR> subscripted </OMSTR>
    </OMATP>
    <OMA>
      <OMS cd=”minmax” name=”min”/>
      <OMA>
        <OMATTR>
          <OMATP>
            <OMS cd="set" name="notin"/>
            <OMV name="x"/>
            <OMV name="B"/>
          </OMATP>
          <OMA>

                           <OMS cd=”arith” name=”power”/>
            <OMV name="x"/>
            <OMI> 2</OMI>
          </OMA>
        </OMATTR>
        <OMV name="x"/>
      </OMA>
    </OMA>
  </OMATTR>
  <OMV name=”x”/>
</OMA>

$ln a$

<apply>
  <ln/>
  <ci> a </ci>
</apply>
 
\ln a
 
<OMA>
  <OMS cd=”transc” name=”ln”/>
  <OMV name=”a”/>
</OMA>

$hármasalapú logaritmus x$

<apply>
  <log/>
  <logbase>
    <cn> 3 </cn7>
  </logbase>
  <ci> x </ci>
</apply>
 
\log_3 x
 
<OMA>
  <OMS cd=”transc” name=”log”/>
  <OMI> 3 </OMI>
  <OMV name=”x”/>
</OMA>

$e az x-ediken$

<apply>
  <exp/>
  <ci> x </ci>
</apply>
 
\exp x
 
<OMA>
  <OMS cd=”transc” name=”exp”/>
  <OMV name=”x”/>
</OMA>

2.5.4. Logikai műveletek

A logikai “és”, “vagy”, “kizáró vagy” és “nem” kifejezések MathML megfelelői rendre az <and/>, az <or/>, az <xor/> és a <not/> elemek. A <not/> elemnek csak egy, a többinek több argumentuma lehet.

Az implikáció leírásához az <implies/> elemet használjuk, melynek két argumentuma van.

A “minden ...-ra/re” kifejezés leírásához a <forall/> elemet, a “létezik olyan ..., hogy” kifejezés leírásához pedig az <exists/> elemet használjuk. Egy <apply> vagy <reln> segítségével mindkettő összekapcsolható egy <condition> elemmel is.

T_EX-ben a fenti logikai műveletek megfelelői az <xor/> kivételével rendre a következő parancsok: \land, \lor, \neg, \Rightarrow, \forall, \exists. Az <xor/> megfelelője az \=\lor összetett parancs.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “and”, “or”, “xor”, “not”, “implies”, “forall”, “exists” beállításával) helyettesítjük. A szükséges CD a “forall” és “exist” esetében “quant”, egyébként “logic”.

$\text{[math]}$

<apply>
  <and/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
a\land b
 
<OMA>
  <OMS cd = "logic" name="and"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<apply>
  <or/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
a\lor b
 
<OMA>
  <OMS cd = "logic" name="or"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<apply>
  <xor/>
  <ci> a </ci>
  <ci> b </ci>
</apply>
 
a\=\lor b
 
<OMA>
  <OMS cd = "logic" name="xor"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<apply>
  <not/>
  <ci> a </ci>
</apply>
 
\neg a
 
<OMA>
  <OMS cd = "logic" name="not"/>
  <OMV name="a"/>
</OMA>

$\text{[math]}$

<reln>
  <implies/>
  <ci> A </ci>
  <ci> B </ci>
</reln>
 
A\Rightarrow B
 
<OMA>
  <OMS cd = "logic" name="implies"/>
  <OMV name="A"/>
  <OMV name="B"/>
</OMA>

$\text{[math]}$

<apply>
  <forall/>
  <bvar>
    <ci> n </ci>
  </bvar>
  <condition>
    <apply>
      <and/>
      <reln>
        <in/>
        <ci> n </ci>
        <ci type="set"> Z </ci>
      </reln>
      <reln>
        <gt/>
        <ci> n </ci>
        <cn> 0 </cn>
      </reln>
    </apply>
  </condition>
  <apply>
    <exists/>
    <bvar>
      <ci> x </ci>
    </bvar>
    <bvar>
      <ci> y </ci>
    </bvar>
    <bvar>
      <ci> z </ci>
    </bvar>
    <condition>
      <apply>
        <reln>
          <in/>
          <ci> x </ci>

                         <ci type="set"> Z </ci>
        </reln>
        <reln>
          <in/>
          <ci> y </ci>
          <ci type="set"> Z </ci>
        </reln>
        <reln>
          <in/>
          <ci> z </ci>
          <ci type="set"> Z </ci>
        </reln>
      </apply>
    </condition>
    <reln>
      <eq/>
      <apply>
        <plus/>
        <apply>
          <power/>
          <ci> x </ci>
          <ci> n </ci>
        </apply>
        <apply>
          <power/>

                         <ci> y </ci>
          <ci> n </ci>
        </apply>
      </apply>
      <apply>
        <power/>
        <ci> z </ci>
        <ci> n </ci>
      </apply>
    </reln>
  </apply>
</apply>
 
\forall n\mid n\in Z\land n>0:\exists x,y,z\mid x,y,z\in Z \Rightarrow
x^n+y^n=z^n
 
<OMA>
  <OMATTR>
    <OMATP>
      <OMS cd="logic" name="and"/>
      <OMA>
        <OMS cd="set" name="in"/>
        <OMV name="n"/>
        <OMV name="Z"/>
      </OMA>
      <OMA>
        <OMS cd="relation" name="gt"/>
        <OMV name="n"/>
        <OMI> 0 </OMI>
      </OMA>
    </OMATP>
    <OMA>

                     <OMS cd="quant" name="forall"/>
      <OMV name="n"/>
    </OMA>
  </OMATTR>
  <OMV name="n"/>
  <OMATTR>
    <OMATP>
      <OMS cd="logic" name="impies"/>
      <OMA>
        <OMS cd="set" name="in"/>
        <OMA>
          <OMS cd="linalg" name="vector"/>
          <OMV name="x"/>
          <OMV name="y"/>
          <OMV name="z"/>
        </OMA>
        <OMV name="Z"/>
      </OMA>
      <OMA>
        <OMS cd="relation" name="eq"/>
        <OMA>
          <OMS cd="arith" name="plus"/>
          <OMA>
            <OMS cd="arith" name="power"/>
            <OMV name="x"/>
            <OMV name="n"/>

                         </OMA>
          <OMA>
            <OMS cd="arith" name="power"/>
            <OMV name="y"/>
            <OMV name="n"/>
          </OMA>
        </OMA>
        <OMA>
          <OMS cd="arith" name="power"/>
          <OMV name="z"/>
          <OMV name="n"/>
        </OMA>
      </OMA>
    </OMATP>
    <OMA>
      <OMS cd="quant" name"exists"/>
      <OMA>
        <OMS cd="linalg" name="vector"/>
        <OMV name="x"/>
        <OMV name="y"/>
        <OMV name="z"/>
      </OMA>
    </OMA>
  </OMATTR>
  <OMS cd="linalg" name="vector"/>
  <OMV name="x"/>
  <OMV name="y"/>
  <OMV name="z"/>
</OMA>

2.5.5. Relációk

Egy reláció leírására a <reln> elemet használjuk. Alkalmazása hasonlít az <apply>-ra. Az elem első utóda mindig az a reláció, amelyet meg szeretnénk valósítani, ezután következnek a reláció argumentumai. Az esetek egy részében a relációk meghatározásakor valamilyen feltételt is szabunk. Ezt a MathML-ben a <condition> elem segítségével tehetjük. Használhatjuk olyan speciális halmazok jelölésére is, ahol a halmaz elemei megszámlálhatatlanok. Egyiknek sincs definitionURL attribútuma!

Magukat a relációkat a következő elemek írják le: <eq/> - “egyenlő”; <neq/> - “nem egyenlő”; <gt/> - “nagyobb, mint”; <lt/> - “kisebb, mint”; <geq/> - “nagyobb vagy egyenlő”; <leq/> - “kisebb vagy egyenlő”.

T_EX-ben magát a relációt és a feltételt írjuk le. A fenti relációknak rendre a következő jelek, illetve parancsok felelnek meg: “=”, \ne, “>”, “<”, \geq, \leq.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “eq”, “neq”, “gt”, “lt”, “geq”, “leq” beállításával) helyettesítjük. A szükséges CD minden esetben a “relation”. A MathML <condition> elem helyettesítése egy <OMATTR> szerkezettel lehetséges.

$\text{[math]}$

<reln>
  <eq/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a=b
 
<OMA>
  <OMS cd="relation" name="eq"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<reln>
  <neq/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a\ne b
 
<OMA>
  <OMS cd="relation" name="neq"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<reln>
  <gt/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a>b
 
<OMA>
  <OMS cd="relation" name="gt"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<reln>
  <lt/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a<b
 
<OMA>
  <OMS cd="relation" name="lt"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<reln>
  <geq/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a\geq b
 
<OMA>
  <OMS cd="relation" name="geq"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<reln>
  <leq/>
  <ci> a </ci>
  <ci> b </ci>
</reln>
 
a\leq b
 
<OMA>
  <OMS cd="relation" name="leq"/>
  <OMV name="a"/>
  <OMV name="b"/>
</OMA>

$\text{[math]}$

<condition>
  <reln>
    <in/>
    <ci> x </ci>
    <ci type="set"> R </ci>
  </reln>
</condition>
 
x\in R
 
<OMA>
  <OMS cd=”set” name=”in”/>
  <OMV name=”x”/>
  <OMV name=”R”/>
</OMA>

$\text{[math]}$

<apply>
  <max/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <condition>
    <apply>
      <and/>
      <reln>
        <gt/>
        <ci> x </ci>
        <cn> 0 </cn>
      </reln>
      <reln>
        <lt/>
        <ci> x </ci>
        <cn> 1 </cn>
      </reln>
    </apply>
  </condition>
  <apply>
    <minus/>
    <ci> x </ci>
    <apply>
      <sin/>
      <ci> x </ci>
    </apply>
  </apply>
</apply>
 
\max\left\{x-\sin x\mid0<x<1\right\}
 
<OMA>
  <OMATTR>
    <OMATP>
      <OMS cd=”presentation” name=”style”/>
      <OMSTR> subscripted </OMSTR>
    </OMATP>
    <OMA>

                     <OMS cd=”minmax” name=”min”/>
      <OMA>
        <OMATTR>
          <OMATP>
            <OMS cd="relation" name="lt"/>
            <OMA>
              <OMS cd="relation" name="lt"/>
              <OMI> 0 </OMI>
              <OMV name="x"/>
            </OMA>
            <OMI> 1 </OMI>
          </OMATP>
          <OMA>
            <OMS cd=”arith” name=”minus”/>
            <OMV name="x"/>
            <OMA>
              <OMS cd="transc" name="sin"/>
              <OMV name="x"/>
            </OMA>

                         </OMA>
        </OMATTR>
        <OMV name="x"/>
      </OMA>
    </OMA>
  </OMATTR>
  <OMV name=”x”/>
</OMA>

2.6. Függvénytan

2.6.1. Felhasználói függvények

Egy felhasználó által készített függvény leírását az <fn> elem segítségével végezhetjük el. Ezen kívül lehetőségünk van egy speciális azonosító-függvény létrehozására is, az <ident/> elemmel.

T_EX-ben ezeknek az elemeknek nincs megfelelője, csak magát a függvényeket írjuk le.

OpenMath-ban egy <OMA> és egy <OMS/> elem kapcsolatával fejezhetjük ki, ahol az <OMS/> elemben írjuk le magát a felhasználói függvényt. Több, egymásba ágyazott függvény esetén az <OMA> elem helyett használhatjuk az <OMBIND>, <OMBVAR/> elempárt is, mely magát az egymásba ágyazást jelöli. Az azonosítót az “fns” CD-beli “identity” attribútummal képezhetjük.

$\text{[math]}$

<fn>
  <ci> L </ci>
</fn>
 
L
 
<OMA>
  <OMS cd=”ecc” name=”type”/>
  <OMS cd=”ecc” name=”function”/>
  <OMV name=”L”/>
</OMA>

$\text{[math]}$

<fn definitionURL="http://www.defs.org/MyDefinition.txt">
  <ci>
    <msub>
      <mi>J</mi>
      <mn>0</mn>
    </msub>
  </ci>
</fn>
 
J_0
 
<OMA>
  <OMATTR>
    <OMATP>
      <OMS cd=”presentation” name=”style”/>
      <OMSTR> subscripted </OMSTR>
    </OMATP>
    <OMA>
      <OMS cd=”ecc” name=”type”/>
      <OMS cd=”ecc” name=”function”/>
      <OMV name=”J”/>
    </OMA>
  </OMATTR>
  <OMI> 0 </OMI>
</OMA>

$\text{[math]}$

<fn>
  <apply>
    <plus/>
    <ci> f </ci>
    <ci> g </ci>
  </apply>
</fn>
 
f+g
 
<OMA>
  <OMS cd=”arith” name=”plus”/>
  <OMA>
    <OMS cd=”ecc” name=”type”/>
    <OMS cd=”ecc” name=”function”/>
    <OMV name=”f”/>
  </OMA>
  <OMA>
    <OMS cd=”ecc” name=”type”/>
    <OMS cd=”ecc” name=”function”/>
    <OMV name=”g”/>
  </OMA>
</OMA>

$\text{[math]}$

<reln>
  <eq/>
  <apply>
    <compose/>
    <fn>
      <ci> f </ci>
    </fn>
    <apply>
      <inverse/>
      <fn>
        <ci> f </ci>
      </fn>
    </apply>
  </apply>
  <ident/>
</reln>
 
f\circ f^{-1}=id
 
<OMA>
  <OMS cd=”relation” name=”eq”/>
  <OMA>
    <OMS cd=”fns” name=”left_compose”/>
    <OMA>
      <OMS cd=”ecc” name=”type”/>
      <OMS cd=”ecc” name=”function”/>
      <OMV name=”f”/>
    </OMA>
    <OMA>
      <OMS cd=”fns” name=”inverse”/>
      <OMA>
        <OMS cd=”ecc” name=”type”/>
        <OMS cd=”ecc” name=”function”/>
        <OMV name=”f”/>
      </OMA>
    </OMA>
  </OMA>

                 <OMA>
    <OMS cd=”fns” name=”identity”/>
    <OMV name=”id”/>
  </OMA>
</OMA>

2.6.2. A lambda függvény

A <lambda> elemet egy olyan felhasználó által meghatározott függvény esetében használjuk, amelyet egy adott kifejezésből és egy vagy több független változóból készítünk. Utódaiban először a változókat kell megadnunk, majd utoljára az aktuális paraméterértékeket.

Ha egy <declare> elem argumentumaként használjuk, akkor meghatározhatjuk a függvény nevét is.

T_EX-ben nincs szükség ilyen parancsra, helyette egyszerűen leírjuk az adott kifejezést (a függvényhez használhatjuk a \lambda parancsot).

OpenMath-ban ezt az elemet az <OMBIND> - <OMBVAR/> elempárossal írhatjuk le. Az <OMBVAR/> elem határozza meg a függvény változóját. A szükséges CD az “fns”.

$\text{[math]}$

<lambda>
  <bvar>
    <ci> x </ci>
  </bvar>
  <apply>
    <sin/>
    <apply>
      <plus/>
      <ci> x </ci>
      <cn> 1 </cn>
    </apply>
  </apply>
</lambda>
 
\lambda\left(x,\sin x+1\right)
 
<OMBIND>
  <OMS cd=”fns” name=”lambda”/>
  <OMBVAR>
    <OMV name=”x”/>
  </OMBVAR>
  <OMA>
    <OMS cd=”transc” name=”sin”/>
    <OMA>
      <OMS cd=”arith” name=”plus”/>
      <OMV name=”x”/>
      <OMI> 1 </OMI>
    </OMA>
  </OMA>
</OMBIND>

2.6.3. Függvényekkel végzett műveletek

Függvények inverzét az <inverse/> elemmel írhatjuk le.

A <compose/> elem segítségével függvények kompozícióját jelölhetjük.

T_EX-ben az inverz-függvénynek nincsen külön parancsa, indexek segítségével írhatjuk le. A függvénykompozíció jelölésére használjuk a \circ parancsot.

OpenMath-ban a fenti műveleteket egy <OMS/> elem megfelelő paraméterezésével (a name attribútum “inverse”, ”left_compose” beállításával) érhetjük el. A szükséges CD az “fns”.

$\text{[math]}$

<apply>
  <inverse definitionURL="MyDefinition.def"/>
  <ci> f </ci>
</apply>
 
f^{-1}
 
<OMA>
  <OMS cd=”fns” name=”inverse”/>
  <OMV name=”f”/>
</OMA>

$\text{[math]}$

<apply>
  <apply>
    <compose/>
    <fn>
      <ci> f </ci>
    </fn>
    <fn>
      <ci> g </ci>
    </fn>
  </apply>
  <ci> x </ci>
</apply>
 
\left(f\circ g\right)\left(x\right)
 
<OMA>
  <OMS cd=”fns” name=”compose”/>
  <OMA>
    <OMATTR>
      <OMATP>
        <OMS cd=”ecc” name=”type”/>
        <OMS cd=”ecc” name=”function”/>
      </OMATP>
      <OMV name=”f”/>
    </OMATTR>
  </OMA>
  <OMA>
    <OMATTR>
      <OMATP>
        <OMS cd=”ecc” name=”type”/>
        <OMS cd=”ecc” name=”function”/>
      </OMATP>
      <OMV name=”g”/>
    </OMATTR>
  </OMA>
  <OMV name=”x”/>
</OMA>

2.7. Integrál- és differenciálszámítás

2.7.1. Integrálszámítás

Az <int/> elemet használjuk az integrál leírásához. A változó megadásához a <bvar> elem szükséges. Az alsó és felső határ megadására több módszer közül választhatunk: az egyik a <lowlimit> és az <uplimit> elemek használata; a másik az <interval> elem használata, ebben az esetben mindkét határt az <interval> elem utódaként kell megadnunk; a harmadik pedig a <condition> elem segítségével, halmazként adjuk meg a határokat.

T_EX-ben az \int parancsot használjuk az integrál leírására. A határokat a \limits parancs után indexek segítségével adjuk meg.

OpenMath-ban az integrál és intervallumának leírására az <OMS/> elemet használhatjuk, a megfelelő paraméterezéssel (a name attribútum “defint”, “interval”; halmazként való megadás esetén “lambda” beállításával). A szükséges CD “defint” esetén “calculus”, “interval”-nál “interval”, “lambda”-nál pedig “fns”.

Példa a <lowlimit>, <uplimit>, és <bvar> használatára:

$\text{[math]}$

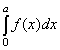
<apply>
  <int/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <lowlimit>
    <cn> 0 </cn>
  </lowlimit>
  <uplimit>
    <ci> a </ci>
  </uplimit>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\int\limits_0^a f(x)dx
 
<OMA>
  <OMS cd=”calculus” name=”defint”/>
  <OMA>
    <OMS cd="interval" name="interval"/>
    <OMI> 0 </OMI>
    <OMV name="a"/>
  </OMA>
  <OMA>
    <OMATTR>
      <OMATP>
        <OMS cd=”ecc” name=”type”/>
        <OMS cd=”ecc” name=”function”/>
      </OMATP>
      <OMV name=”f”/>
    </OMATTR>
    <OMV name=”x”/>
  </OMA>
</OMA>

Példa az <interval> használatára:

$\text{[math]}$

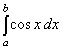
<apply>
  <int/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <interval>
    <ci> a </ci>
    <ci> b </ci>
  </interval>
  <apply>
    <cos/>
    <ci> x </ci>
  </apply>
</apply>
 
\int\limits_a^b \cos x dx
 
<OMA>
  <OMS cd=”calculus” name=”defint”/>
  <OMA>
    <OMS cd="interval" name="interval"/>
    <OMV name="a"/>
    <OMV name="b"/>
  </OMA>
  <OMA>
    <OMS cd="transc" name="cos"/>
    <OMV name="x"/>
  </OMA>
</OMA>

Példa a <condition> használatára:

$\text{[math]}$

<apply>
  <int/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <condition>
    <reln>
      <in/>
      <ci> x </ci>
      <ci type="set"> D </ci>
    </reln>
  </condition>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\int\limits_{x\in D} f(x)dx
 
<OMA>
  <OMS cd=”calculus” name=”defint”/>
  <OMV name="D"/>
  <OMBIND>
    <OMS cd="fns" name="lambda"/>
    <OMBVAR>
      <OMV name="x"/>
    </OMBVAR>
    <OMA>
      <OMATTR>
        <OMATP>
          <OMS cd=”ecc” name=”type”/>
          <OMS cd=”ecc” name=”function”/>
        </OMATP>
        <OMV name=”f”/>
      </OMATTR>

                     <OMV name=”x”/>
    </OMA>
  </OMBIND>
</OMA>

2.7.2. Differenciálszámítás

A <diff/> elemet használjuk a differenciálhányados leírásához. A változó megadásához a <bvar> elem szükséges.

A parciális differenciál leírásához a <partialdiff/> elemet használjuk. A változó megadásához a <bvar> elem szükséges. Ez a <bvar> tartalmazhat egy <degree> elemet is mellyel a parciális derivált foka adható meg.

T_EX-ben nincs rá külön parancs, a kifejezést egyszerűen leírjuk. Egyedül a δ jelnek van speciális megjelenítése, ez a \partial parancs.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “diff” vagy “partialdiff” beállításával) helyettesítjük. A szükséges CD a “calculus”.

$\text{[math]}$

<apply>
  <diff/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\frac d{dx} f(x)
 
<OMA>
  <OMS cd=”calculus” name=”diff”/>
  <OMV name=”x”/>
  <OMA>
    <OMATTR>
      <OMATP>
        <OMS cd=”ecc” name=”type”/>
        <OMS cd=”ecc” name=”function”/>
      </OMATP>
      <OMV name=”f”/>
    </OMATTR>
    <OMV name=”x”/>
  </OMA>
</OMA>

$\text{[math]}$

<apply>
  <partialdiff/>
  <bvar>
    <ci> x </ci>
    <degree>
      <cn> 2 </cn>
    </degree>
  </bvar>
  <bvar>
    <ci> y </ci>
  </bvar>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
    <ci> y </ci>
  </apply>
</apply>
 
\frac{\partial^2}{\partial x^2}\frac{\partial}{\partial y} f(x,y)
 
<OMA>
  <OMA>
    <OMS cd="calculus" name="partialdiff"/>
    <OMBIND>
      <OMS cd="fns" name="lambda"/>
      <OMBVAR>
        <OMV name="x"/>
      </OMBVAR>
      <OMBVAR>
        <OMV name="y"/>
      </OMBVAR>
      <OMA>
        <OMV name="f"/>
        <OMATTR>
          <OMATP>
            <OMS cd="presentation" name="left"/>

                           <OMSTR>(</OMSTR>
            <OMS cd="presentation" name="right"/>
            <OMSTR>)</OMSTR>
          </OMATP>
          <OMV name="x"/>
          <OMV name="y"/>
        </OMATTR>
      </OMA>
    </OMBIND>
  </OMA>
  <OMV name="x"/>
  <OMV name="y"/>
</OMA>

2.8. Halmazelmélet

2.8.1. Halmazok megadása

A <set> elemet használjuk általában a halmazok leírásához. Ha a halmaz elemeinek sorrendje is fontos, akkor a <list> elemet használjuk. A halmazokat vagy felsorolással, vagy a <bvar> és a <condition> elemek segítségével adhatjuk meg. A <set>-nél megadható a type argumentum, értékei “normal” és “multiset”, ez utóbbi megengedi az elemek ismétlődését, alapértelmezés a “normal”. A <list> saját attribútuma az order, mellyel a sorrend típusát adhatjuk meg, két értéket vehet fel, a sorrend lehet “lexicographic” vagy “numeric”, alapértelmezés az utóbbi.

Egyiknek sincs definitionURL attribútuma!

Hogy egy adott elem része-e a halmaznak, azt az <in/> és a <notin/> elemmel írhatjuk le. Mindkettőnek két argumentuma van.

T_EX-ben a halmazok megadására nincs külön parancs, a halmazok elemeit és egyéb paramétereit egyszerűen leírjuk. Az “eleme”, “nem eleme” kifejezéseket az \in, \notin parancsokkal írhatjuk le.

OpenMath-ban a halmazok megadását az <OMS/> elem megfelelő paraméterezésével (a name attribútum “set”, “list”, “in”, “notin” beállításával) végezzük el. A szükséges CD “list” esetén “list”, egyébként ”set”.

$\text{[math]}$

<set>
  <ci> b </ci>
  <ci> a </ci>
  <ci> c </ci>
</set>
 
\left\{a,b,c\right\}
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>{</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>}</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd = "set" name="set"/>
    <OMV name="a"/>
    <OMV name="b"/>
    <OMV name="c"/>
  </OMA>
</OMATTR>

$\text{[math]}$

<set>
  <bvar>
    <ci> x </ci>
  </bvar>
  <condition>
    <reln>
      <lt/>
      <ci> x </ci>
      <cn> 5 </cn>
    </reln>
  </condition>
</set>
 
\left\{x\mid x<5\right\}
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>{</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>}</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd="relation" name="lt"/>
    <OMV name="x"/>
    <OMI> 5 </OMI>
</OMATTR>

$\text{[math]}$

<list>
  <ci> b </ci>
  <ci> a </ci>
  <ci> c </ci>
</list>
 
\left\[a,b,c\right\]
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>[</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>]</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd = "set" name="set"/>
    <OMV name="a"/>
    <OMV name="b"/>
    <OMV name="c"/>
  </OMA>
</OMATTR>

$\text{[math]}$

<list order="numeric">
  <bvar>
    <ci> x </ci>
  </bvar>
  <condition>
    <reln>
      <lt/>
      <ci> x </ci>
      <cn> 5 </cn>
    </reln>
  </condition>
</list>
 
\left\[x\mid x<5\right\]
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>[</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>]</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd="relation" name="lt"/>
    <OMV name="x"/>
    <OMI> 5 </OMI>
  </OMA>
</OMATTR>

$\text{[math]}$

<reln>
  <in/>
  <ci> a </ci>
  <ci type="set"> A </ci>
</reln>
 
a\in A
 
<OMA>
  <OMS cd=”set” name=”in”/>
  <OMV name=”a”/>
  <OMV name=”A”/>
</OMA>

$\text{[math]}$

<reln>
  <notin/>
  <ci> a </ci>
  <ci> A </ci>
</reln>
 
a\notin A
 
<OMA>
  <OMS cd=”set” name=”notin”/>
  <OMV name=”a”/>
  <OMV name=”A”/>
</OMA>

2.8.2. Halmazműveletek

A MathML-ben a következő halmazműveletek ismertek: <union/> - “unió”; <intersect/> - “metszet”; <subset/> - “részhalmaz”; <prsubset/> - “valódi részhalmaz”; <notsubset/> - “nem részhalmaza”; <notprsubset/> - “nem valódi részhalmaza”; <setdiff/> - “különbség”. Az <union/>-nak és az <intersect/>-nek több, a maradéknak két argumentuma lehet.

A fenti elemek T_EX megfelelői: \cup, \cap, \subseteq, \subset, \not\subseteq, \not\subset, \setminus.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “union”, “intersect”, “subset”, “notsubset”, “prsubset”, “notprsubset”, “setdiff” beállításával) helyettesítjük. A szükséges CD minden esetben a “set”.

$\text{[math]}$

<apply>
  <union/>
  <ci> A </ci>
  <ci> B </ci>
</apply>
 
A\cup B
 
<OMA>
  <OMS cd=”set” name=”union”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

$\text{[math]}$

<apply>
  <intersect/>
  <ci type="set"> A </ci>
  <ci type="set"> B </ci>
</apply>
 
A\cap B
 
<OMA>
  <OMS cd=”set” name=”intersect”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

$\text{[math]}$

<reln>
  <subset/>
  <ci> A </ci>
  <ci> B </ci>
</reln>
 
A\subseteq B
 
<OMA>
  <OMS cd=”set” name=”subset”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

$\text{[math]}$

<reln>
  <prsubset/>
  <ci> A </ci>
  <ci> B </ci>
</reln>
 
A\subset B
 
<OMA>
  <OMS cd=”set” name=”prsubset”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
  </OMA>

$\text{[math]}$

<reln>
  <notsubset/>
  <ci> A </ci>
  <ci> B </ci>
  </reln>
 
A\not\subseteq B
 
<OMA>
  <OMS cd=”set” name=”notsubset”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

$\text{[math]}$

<reln>
  <notprsubset/>
  <ci> A </ci>
  <ci> B </ci>
</reln>
 
A\not\subset B
 
<OMA>
  <OMS cd=”set” name=”notprsubset”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

$\text{[math]}$

<apply>
  <setdiff/>
  <ci> A </ci>
  <ci> B </ci>
</apply>
 
A\setminus B
 
<OMA>
  <OMS cd=”set” name=”setdiff”/>
  <OMV name=”A”/>
  <OMV name=”B”/>
</OMA>

2.9. Sorozatok

Egy sorozat határértékének leírásához a <limit/> elemet használjuk. A határpont megadása a <lowlimit> elemmel, vagy a <condition> elemmel lehetséges. Az összegzés indexét a <bvar> elemmel adhatjuk meg.

Azt, hogy egy adott sorozat mihez tart, azt a <tendsto/> elem segítségével adjuk meg, melynek két argumentuma van. Az irányt a type attribútummal határozhatjuk meg, melynek értékei a következők lehetnek: “above”, “bellow”, “two-sided”, alapértelmezése az “above”.

Egy sorozat elemeinek összegzéséhez, a szumma leírásához a <sum/> elemet használjuk. A <product/> elemet használjuk a sorozat elemeinek szorzatának, a produktum leírásához. Mindkettőnél a felső és alsó határ megadása az <int/> elemnél megismert módon vagy <uplimit> és <lowlimit> elemekkel, vagy a <condition> elemmel lehetséges. Az összegzés indexét a <bvar> elemmel adhatjuk meg.

T_EX-ben a határérték leírására a \lim parancsot használjuk, mely után, a \limits és a \to parancs párral adhatjuk meg hogy a határérték mihez tart. A MathML <tendsto/> elemének megfelelői T_EX-ben iránytól és nagyságtól függően a következők: \leftarrow, \rightarrow, \leftrightarrow; \longleftarrow, \longrightarrow, \longleftrightarrow.

A szumma és a produktum leírása a \sum és \prod parancsokkal történik, melyek után kiemelt matematikai módban indexekkel, egyébként a \limits paranccsal lehet megadni a kívánt határokat.

A végtelen (∞) leírására használjuk az \infty parancsot.

OpenMath-ban a fenti elemeket az <OMS/> elem megfelelő paraméterezésével (a name attribútum “limit”, “sum”, “product” beállításával) helyettesítjük. A <tendsto/> megfelelői az <OMS>-ban a name attribútum “above”, “below”, “both_sides” beállításai. A “sum” és “product” beállításnál az intervallum leírására szintén egy <OMS/> elem megfelelő paraméterezése (a name attribútum “interval”; halmazként való megadás esetén “lambda” beállításával) használatos. A szükséges CD a “sum”, “product” műveleteknél az “arith”, “interval”-nál “interval”, “lambda”-nál “fns”, a többinél a “limit”.

A végtelen megfelelője az “infinity”, mely a “nums” CD-ben található.

$\text{[math]}$

<apply>
  <limit/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <lowlimit>
    <cn> 0 </cn>
  </lowlimit>
  <apply>
    <sin/>
    <ci> x </ci>
</apply>
</apply>
 
\lim\limits_{n \to 0}\sin x
 
<OMA>
  <OMS cd=”limit” name=”limit”/>
  <OMA>
    <OMS cd=”transc” name=”sin”/>
    <OMV name=”x”/>
  </OMA>
</OMA>

$\text{[math]}$

<reln>
  <tendsto type="above"/>
  <apply>
    <power/>
    <ci> x </ci>
    <cn> 2 </cn>
  </apply>
  <apply>
    <power/>
    <ci> a </ci>
    <cn> 2 </cn>
  </apply>
</reln>
 
x^2\rightarrow a^2
 
<OMA>
  <OMS cd = "limit" name="above"/>
  <OMA>
    <OMS cd="arith" name="power"/>
    <OMV name="x"/>
    <OMI>2</OMI>
  </OMA>
  <OMA>
    <OMS cd="arith" name="power"/>
    <OMV name="a"/>
    <OMI>2</OMI>
  </OMA>
</OMA>

$\text{[math]}$

<apply>
  <sum/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <lowlimit>
    <ci> a </ci>
  </lowlimit>
  <uplimit>
    <ci> b </ci>
  </uplimit>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\sum\limits_{x=a}^b f(x)
 
<OMA>
  <OMS cd="arith" name="sum"/>
  <OMA>
    <OMS cd="interval" name="integer-interval"/>
    <OMV name="a"/>
    <OMV name="b"/>
  </OMA>
  <OMBIND>
    <OMS cd="fns" name="lambda"/>
    <OMBVAR>
      <OMV name="x"/>
    </OMBVAR>
    <OMA>
      <OMV name="f"/>
      <OMATTR>
        <OMATP>
          <OMS cd="presentation" name="left"/>
          <OMSTR>(</OMSTR>
          <OMS cd="presentation" name="right"/>
          <OMSTR>)</OMSTR>

                       </OMATP>
        <OMV name="x"/>
      </OMATTR>
    </OMA>
  </OMBIND>
</OMA>

$\text{[math]}$

<apply>
  <product/>
  <bvar>
    <ci> x </ci>
  </bvar>
  <condition>
    <reln>
      <in/>
      <ci> x </ci>
      <ci type="set"> B </ci>
    </reln>
  </condition>
  <apply>
    <fn>
      <ci> f </ci>
    </fn>
    <ci> x </ci>
  </apply>
</apply>
 
\prod_{x\in B} f(x)
 
<OMA>
  <OMS cd="arith" name="product"/>
  <OMV name="B"/>
  <OMBIND>
    <OMS cd="fns" name="lambda"/>
    <OMBVAR>
      <OMV name="x"/>
    </OMBVAR>
    <OMA>
      <OMV name="f"/>
      <OMATTR>
        <OMATP>
          <OMS cd="presentation" name="left"/>
          <OMSTR>(</OMSTR>
          <OMS cd="presentation" name="right"/>
          <OMSTR>)</OMSTR>
        </OMATP>

                       <OMV name="x"/>
      </OMATTR>
    </OMA>
  </OMBIND>
</OMA>

2.10. Trigonometria

A trigonometriai függvények széles körben ismertek, ezért külön-külön történő ismertetésüktől eltekintek, de álljon itt felsorolásuk:

<sin/>, <cos/>, <tan/>, <cot/>, <sec/>, <csc/>, <sinh/>, <cosh/>, <tanh/>, <coth/>, <sech/>, <csch/>, <arcsin/>, <arccos/>, <arctan/>

Minden trigonometriai elemnek egyetlen argumentuma van.

T_EX-ben a fenti elemeknek megfelelő parancsok rendre: \sin, \cos, \tan, \cot, \sec, \csc, \sinh, \cosh, \tanh, \coth, \arcsin, \arccos, \arctan. A <sech/> és a <csch/> elemeknek nincsenek megfelelői.

OpenMath-ban a trigonometriai elemeket egy <OMS/> elem name attribútumában adhatjuk meg. A szögfüggvények nevei megegyeznek a fenti nevekkel. A trigonometriai függvényeket tartalmazó CD neve “transc”.

$\text{[math]}$

<apply>
  <sin/>
  <ci> x </ci>
</apply>
 
\sin x
 
<OMA>
  <OMS cd=”transc” name=”sin”/>
  <OMV name=”x”/>
</OMA>

$\text{[math]}$

<apply>
  <sin/>
  <apply>
    <plus/>
    <apply>
      <cos/>
      <ci> x </ci>
    </apply>
    <apply>
      <power/>
      <ci> x </ci>
      <cn> 3 </cn>
    </apply>
  </apply>
</apply>
 
\sin(\cos x+x^3)
 
<OMA>
  <OMS cd="transc" name="sin"/>
  <OMATTR>
    <OMATP>
      <OMS cd="presentation" name="left"/>
      <OMSTR>(</OMSTR>
      <OMS cd="presentation" name="right"/>
      <OMSTR>)</OMSTR>
    </OMATP>
    <OMA>
      <OMS cd = "arith" name="plus"/>
      <OMA>
        <OMS cd="transc" name="cos"/>
        <OMV name="x"/>
      </OMA>
      <OMA>
        <OMS cd="arith" name="power"/>
        <OMV name="x"/>
        <OMI>3</OMI>
      </OMA>

                   </OMA>
  </OMATTR>
</OMA>

2.11. Statisztika

A statisztikai műveletek közül a következőket találjuk meg MathML-ben: <mean/> - átlag; <sdev/> - szórás; <variance/> - szórásnégyzet; <median/> - medián; <mode/> - módusz; <moment/> - statisztikai momentum. Ez utóbbinál a momentum fokát a <degree> elemmel határozhatjuk meg.

T_EX-ben a fenti elemeknek nincsenek megfelelői.

OpenMath-ban a fenti elemek leírására az <OMS/> elemet használhatjuk, a megfelelő paraméterezéssel (a name attribútum “mean”, “sdev”, “variance”, “median”, “mode”, “moment” beállításával). A szükséges CD a “stats”.

$\text{[math]}$

<apply>
  <mean/>
  <ci> X </ci>
</apply>
 
\overline X
 
<OMA>
  <OMS cd=”stats” name=”mean”/>
  <OMV name=”X”/>
</OMA>

$\text{[math]}$

<apply>
  <sdev/>
  <ci> X </ci>
</apply>
 
\sigma(X)
 
<OMA>
  <OMS cd=”stats” name=”sdev”/>
  <OMV name=”x”/>
</OMA>

$\text{[math]}$

<apply>
  <variance/>
  <ci> X </ci>
</apply>
 
\sigma^2 (X)
 
<OMA>
  <OMS cd=”stats” name=”variance”/>
  <OMV name=”x”/>
</OMA>

$\text{[math]}$

<apply>
  <median/>
  <ci> X </ci>
</apply>
 
\rm{median}(X)
 
<OMA>
  <OMS cd=”stats” name=”median”/>
  <OMV name=”x”/>
</OMA>

$\text{[math]}$

<apply>
  <mode/>
  <ci> X </ci>
</apply>
 
\m{mode}(X)
 
<OMA>
  <OMS cd=”stats” name=”mode”/>
  <OMV name=”x”/>
</OMA>

$\text{[math]}$

<apply>
  <moment/>
  <degree>
    <cn> 3 </cn>
  </degree>
  <ci> X </ci>
</apply>
 
\left\langle X^3\right\rangle
 
<OMA>
  <OMS cd=”stats” name=”moment”/>
  <OMV name=”x”/>
</OMA>

2.12. Lineáris algebra

2.12.1. Vektorok

A <vector> elemet használjuk a vektorok leírásához. Argumentumai írják le a vektor komponenseit. A vektorok tartalmilag egy egysoros mátrixhoz hasonlíthatók.

T_EX-ben nincs megfelelője.

OpenMath-ban a vektorok leírására az <OMS/> elemet használhatjuk, a megfelelő paraméterezéssel (a name attribútum “vector” beállításával). A szükséges CD a “linalg”.

$\text{[math]}$

<vector>
  <cn> 1 </cn>
  <cn> 2 </cn>
  <cn> 3 </cn>
  <ci> x </ci>
</vector>
 
\left(1,2,3,x\right)
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>(</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>)</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd = "linalg" name="vector"/>
    <OMI>1</OMI>
    <OMI>2</OMI>
    <OMI>3</OMI>
    <OMV name="x"/>
  </OMA>
</OMATTR>

2.12.2. Mátrixok

A mátrixok leírásához a <matrix> elemet használjuk. Argumentumai csak <matrixrow> elemek lehetnek, ezek írják le a mátrix sorait.

T_EX-ben a megjelenítő elemek táblákkal és mátrixokkal foglalkozó fejezetében leírtak érvényesek itt is.

OpenMath-ban a mátrixok leírására az <OMS/> elemet használhatjuk, a megfelelő paraméterezéssel (a name attribútum beállításával: a “matrix” írja le magát a mátrixot, a “matrixrow” pedig a mátrix sorait). A szükséges CD a “linalg”.

$\text{[math]}$

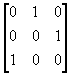
<matrix>
  <matrixrow>
    <cn> 0 </cn>
    <cn> 1 </cn>
    <cn> 0 </cn>
  </matrixrow>
  <matrixrow>
    <cn> 0 </cn>
    <cn> 0 </cn>
    <cn> 1 </cn>
  </matrixrow>
  <matrixrow>
    <cn> 1 </cn>
    <cn> 0 </cn>
    <cn> 0 </cn>
  </matrixrow>
</matrix>
 
\bmatrix 0&1&0\\0&0&1\\1&0&0\endbmatrix
 
<OMATTR>
  <OMATP>
    <OMS cd="presentation" name="left"/>
    <OMSTR>[</OMSTR>
    <OMS cd="presentation" name="right"/>
    <OMSTR>]</OMSTR>
  </OMATP>
  <OMA>
    <OMS cd = "linalg" name="matrix"/>
    <OMA>
      <OMS cd = "linalg" name="matrixrow"/>
      <OMI>0</OMI>
      <OMI>1</OMI>
      <OMI>0</OMI>
    </OMA>
    <OMA>
      <OMS cd = "linalg" name="matrixrow"/>
      <OMI>0</OMI>

                     <OMI>0</OMI>
      <OMI>1</OMI>
    </OMA>
    <OMA>
      <OMS cd = "linalg" name="matrixrow"/>
      <OMI>1</OMI>
      <OMI>0</OMI>
      <OMI>0</OMI>
    </OMA>
  </OMA>
</OMATTR>

2.12.3. Mátrixműveletek

A determinánsok leírására a <determinant/> elemet használjuk. Egy mátrix transzponáltját a <transpose/> elemmel írjuk le.

A <selector/> elemet használjuk egy mátrix, vektor vagy lista elemeinek kiválasztásához. Argumentumai közül az első mindig az objektumot határozza meg, a második kiválasztja az objektum elemét, mátrixok esetén a sort, harmadiknak csak mátrix esetén van értelme (egyébként nem vesszük figyelembe), a megadott sor oszlopát jelöli ki. Mátrix esetén, ha a harmadik argumentum nincs megadva, akkor hatása az egész sorra vonatkozik.

T_EX-ben csak a determináns leírására van parancs, ez pedig a \det. A transzponált leírását egyszerűen indexeléssel írjuk le. A <selector/> elemnek nincs megfelelője, mivel ezt csak számítógépes algebrában használjuk.

OpenMath-ban a fenti elemek leírására az <OMS/> elemet használhatjuk, a megfelelő paraméterezéssel (a name attribútum “determinant”, “transpose”, “selector” beállításával). A szükséges CD a “linalg”.

$\text{[math]}$

<apply>
  <determinant/>
  <ci type="matrix"> A </ci>
</apply>
 
\det\rm\bf A
 
<OMA>
  <OMS cd=”linalg” name=”determinant”/>
  <OMV name=”A”/>
</OMA>

$\text{[math]}$

<apply>
  <transpose/>
  <ci type="matrix"> A </ci>
</apply>
 
A^T
 
<OMA>
  <OMS cd=”linalg” name=”transpose”/>
  <OMV name=”x”/>
</OMA>

A következő példában

<apply>
  <selector/>
  <matrix>
    <matrixrow>
      <cn> 1 </cn>
      <cn> 2 </cn>
    </matrixrow>
    <matrixrow>
      <cn> 3 </cn>
      <cn> 4 </cn>
    </matrixrow>
  </matrix>
  <cn> 1 </cn>
</apply>
 
<OMA>
  <OMS cd=”linalg” name=”selector”/>
  <OMI> 1 </OMI>
  <OMATTR>
    <OMATP>
      <OMS cd="presentation" name="left"/>
      <OMSTR>[</OMSTR>
      <OMS cd="presentation" name="right"/>
      <OMSTR>]</OMSTR>
    </OMATP>
    <OMA>
      <OMS cd = "linalg" name="matrix"/>
      <OMA>
        <OMS cd = "linalg" name="matrixrow"/>
        <OMI>1</OMI>
        <OMI>2</OMI>
      </OMA>
      <OMA>
        <OMS cd = "linalg" name="matrixrow"/>

                       <OMI>3/OMI>
        <OMI>4</OMI>
      </OMA>
    </OMA>
  </OMATTR>
</OMA>

mivel csak két argumentumunk van, a mátrix első sora lesz kiválasztva:

<matrixrow>
  <cn> 1 </cn>
  <cn> 2 </cn>
</matrixrow>
 
<OMA>
  <OMS cd = "linalg" name="matrixrow"/>
  <OMI>1</OMI>
  <OMI>2</OMI>
</OMA>

2.13. Szemantikai elemek

A <semantics> elemet többletinformációk hozzáfűzésére használjuk. Első argumentuma mindig egy MathML kódú kifejezés, amihez a megjegyzést fűzzük. A következő argumentumoknak kötelezően <annotation> vagy <annotation-xml> elemmel kell kezdődniük, ezek írják le magát a megjegyzést. A két elem között az a különbség, hogy az elsőben csak nem XML-alapú leírást adhatunk meg, a másodikban viszont csak XML-alapút. Egy saját attribútumuk van, az encoding, melyben meghatározhatjuk, hogy az adott megjegyzés milyen formátumú. Alapértelmezése “”, vagyis nincs meghatározva.

Általában a kifejezés úgy jelenik meg, ahogyan azt az első argumentumban leírtuk. Esetenként a megjelenítő figyelembe veheti a hozzáfűzött információt, ezt elsősorban a tartalmi és megjelenítő elemek keverésekor használhatjuk ki.

A szemantikai elemeknek nincsenek megfelelőik sem T_EX-ben, sem OpenMath-ban, viszont egy MathML kódhoz ezekkel az elemekkel kapcsolhatunk T_EX és OpenMath kódokat is.

A következő példa azt mutatja be, hogy a $\text{[math]}$ kifejezést és különböző formátumú értelmezéseit hogyan valósíthatjuk meg:

<semantics>
  <apply>
    <plus/>
    <apply>
      <sin/>
      <ci> x </ci>
    </apply>
    <cn> 5 </cn>
  </apply>
  <annotation encoding="TEX">
    \sin x + 5
  </annotation>
  <annotation-xml encoding="OpenMath">
    <OMA>
      <OMS cd=”arith” name="plus"/>
      <OMA>
        <OMS cd=”transc” name="sin"/>
        <OMV name="x"/>
      </OMA>
      <OMI> 5 </OMI>
    </OMA>
  </annotation-xml>
</semantics>

<<< Előző | Következő >>>

mathml.gaja.hu

A matematika elektronikus dokumentálása:MathML, OpenMath vagy T_EX?

III. rész: Részletes összehasonlítás (folytatás)

2. A tartalmi jelölés

2.1. A tartalmi jelölés elemeiről általában

2.2. Tokenelemek

2.2.1. Számok

2.2.2. Azonosítók

2.3. Tartalmi elemek csoportba rendezése

2.4. Deklarációk

2.5. Aritmetika, algebra, logika

2.5.1. Alapműveletek

2.5.2. Fontosabb aritmetikai, algebrai műveletek

2.5.3. Fontosabb aritmetikai, algebrai függvények

2.5.4. Logikai műveletek

2.5.5. Relációk

2.6. Függvénytan

2.6.1. Felhasználói függvények

2.6.2. A lambda függvény

2.6.3. Függvényekkel végzett műveletek

2.7. Integrál- és differenciálszámítás

2.7.1. Integrálszámítás

2.7.2. Differenciálszámítás

2.8. Halmazelmélet

2.8.1. Halmazok megadása

2.8.2. Halmazműveletek

2.9. Sorozatok

2.10. Trigonometria

2.11. Statisztika

2.12. Lineáris algebra

2.12.1. Vektorok

2.12.2. Mátrixok

2.12.3. Mátrixműveletek

2.13. Szemantikai elemek

mathml.gaja.hu

A matematika elektronikus dokumentálása:MathML, OpenMath vagy TEX?

III. rész: Részletes összehasonlítás (folytatás)

2. A tartalmi jelölés

2.1. A tartalmi jelölés elemeiről általában

2.2. Tokenelemek

2.2.1. Számok

2.2.2. Azonosítók

2.3. Tartalmi elemek csoportba rendezése

2.4. Deklarációk

2.5. Aritmetika, algebra, logika

2.5.1. Alapműveletek

2.5.2. Fontosabb aritmetikai, algebrai műveletek

2.5.3. Fontosabb aritmetikai, algebrai függvények

2.5.4. Logikai műveletek

2.5.5. Relációk

2.6. Függvénytan

2.6.1. Felhasználói függvények

2.6.2. A lambda függvény

2.6.3. Függvényekkel végzett műveletek

2.7. Integrál- és differenciálszámítás

2.7.1. Integrálszámítás

2.7.2. Differenciálszámítás

2.8. Halmazelmélet

2.8.1. Halmazok megadása

2.8.2. Halmazműveletek

2.9. Sorozatok

2.10. Trigonometria

2.11. Statisztika

2.12. Lineáris algebra

2.12.1. Vektorok

2.12.2. Mátrixok

2.12.3. Mátrixműveletek

2.13. Szemantikai elemek

A matematika elektronikus dokumentálása:MathML, OpenMath vagy T_EX?